Unsupervised Learning

Unsupervised machine learning refers to the category of machine learning techniques where models are trained on a dataset without labels.

Author

Juma Shafara

Published

February 1, 2024

Modified

July 25, 2024

Keywords

Introduction to Unsupervised Learning, Clustering, K Means Clustering, what number of clusters is good enough

The following topics are covered in this tutorial:

Overview of unsupervised learning algorithms in Scikit-learn.
K Means clustering

Let’s install the required libraries.

# # uncomment and run this cell to install the packages and libraries
# !pip install dataidea

Introduction to Unsupervised Learning

Unsupervised machine learning refers to the category of machine learning techniques where models are trained on a dataset without labels. Unsupervised learning is generally use to discover patterns in data and reduce high-dimensional data to fewer dimensions. Here’s how unsupervised learning fits into the landscape of machine learning algorithms(source):

Here are the topics in machine learning that we’re studying in this course (source):

Scikit-learn offers the following cheatsheet to decide which model to pick for a given problem. Can you identify the unsupervised learning algorithms?

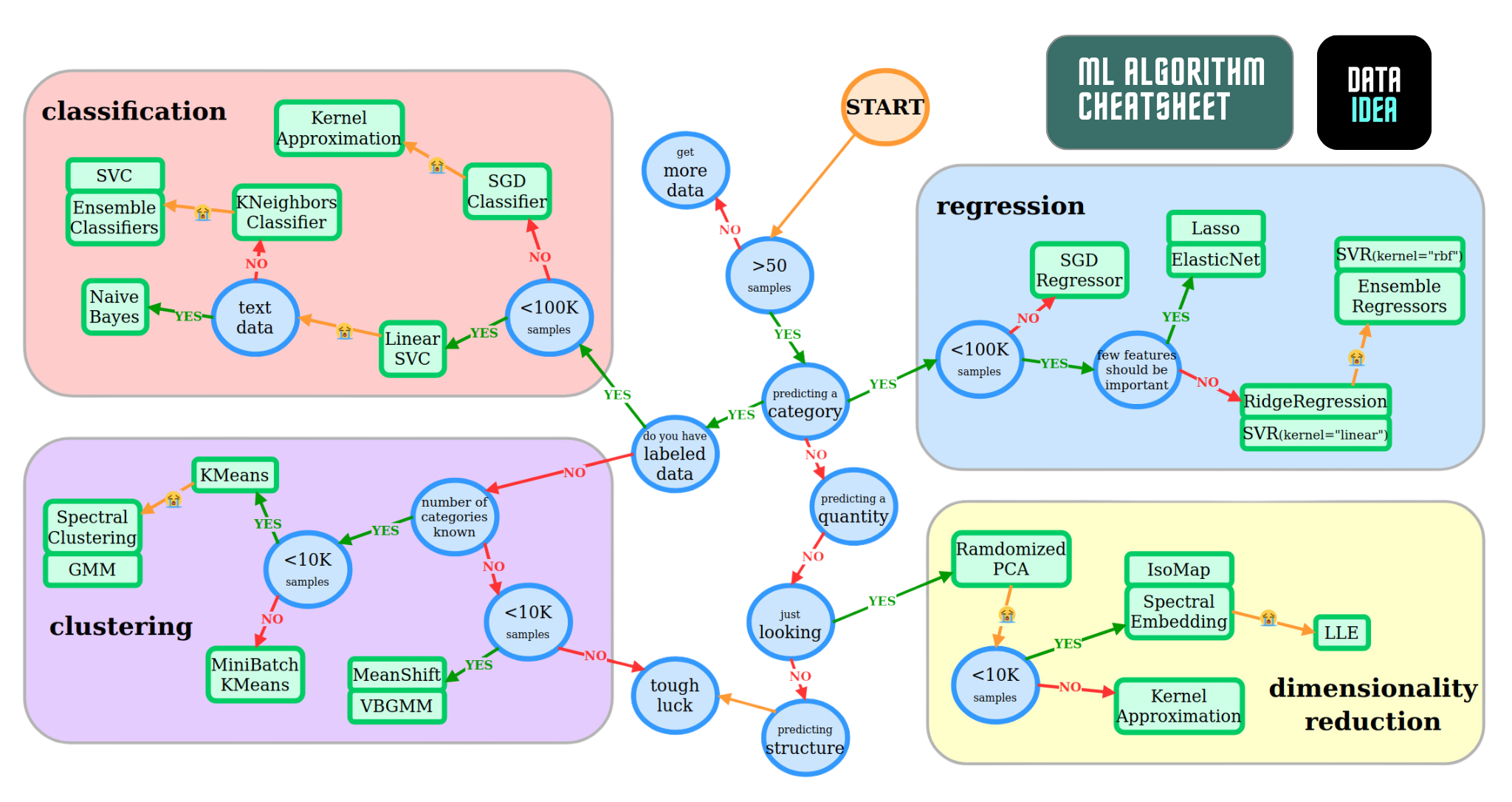
Here is a full list of unsupervised learning algorithms available in Scikit-learn: https://scikit-learn.org/stable/unsupervised_learning.html

Clustering

Clustering is the process of grouping objects from a dataset such that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (Wikipedia). Scikit-learn offers several clustering algorithms. You can learn more about them here: https://scikit-learn.org/stable/modules/clustering.html

Here is a visual representation of clustering:

Here are some real-world applications of clustering:

Customer segmentation
Product recommendation
Feature engineering
Anomaly/fraud detection
Taxonomy creation

We’ll use the Iris flower dataset to study some of the clustering algorithms available in scikit-learn. It contains various measurements for 150 flowers belonging to 3 different species.

import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

sns.set_style('darkgrid')

Let’s load the popular iris and penguin datasets. These datasets are already built in seaborn

# load the iris dataset
iris_df = sns.load_dataset('iris')
iris_df.head()

	sepal_length	sepal_width	petal_length	petal_width	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa

sns.scatterplot(data=iris_df, x='sepal_length', y='petal_length', hue='species')
plt.title('Flower Petal Length against Sepal Length per Species')
plt.ylabel('Petal Length')
plt.xlabel('Sepal Length')
plt.show()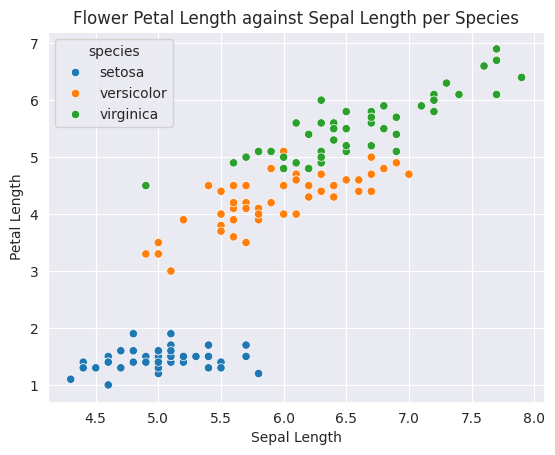

We’ll attempt to cluster observations using numeric columns in the data.

numeric_cols = ["sepal_length", "sepal_width", "petal_length", "petal_width"]
X = iris_df[numeric_cols]
X.head()

	sepal_length	sepal_width	petal_length	petal_width
0	5.1	3.5	1.4	0.2
1	4.9	3.0	1.4	0.2
2	4.7	3.2	1.3	0.2
3	4.6	3.1	1.5	0.2
4	5.0	3.6	1.4	0.2

K Means Clustering

The K-means algorithm attempts to classify objects into a pre-determined number of clusters by finding optimal central points (called centroids) for each cluster. Each object is classifed as belonging the cluster represented by the closest centroid.

Here’s how the K-means algorithm works:

Pick K random objects as the initial cluster centers.
Classify each object into the cluster whose center is closest to the point.
For each cluster of classified objects, compute the centroid (mean).
Now reclassify each object using the centroids as cluster centers.
Calculate the total variance of the clusters (this is the measure of goodness).
Repeat steps 1 to 6 a few more times and pick the cluster centers with the lowest total variance.

Here’s a video showing the above steps:

Let’s apply K-means clustering to the Iris dataset.

from sklearn.cluster import KMeans

model = KMeans(n_clusters=3, random_state=42)
# training the model
model.fit(X)

KMeans(n_clusters=3, random_state=42)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

We can check the cluster centers for each cluster.

We can now classify points using the model.

# making predictions on X (clustering)
preds = model.predict(X)

# assign each row to their cluster
X['clusters'] = preds
# looking at some samples
X.tail(n=5)

	sepal_length	sepal_width	petal_length	petal_width	clusters
145	6.7	3.0	5.2	2.3	0
146	6.3	2.5	5.0	1.9	2
147	6.5	3.0	5.2	2.0	0
148	6.2	3.4	5.4	2.3	0
149	5.9	3.0	5.1	1.8	2

Let’s use seaborn and pyplot to visualize the clusters

sns.scatterplot(data=X, x='sepal_length', y='petal_length', hue=preds)
centers_x, centers_y = model.cluster_centers_[:,0], model.cluster_centers_[:,2]
plt.plot(centers_x, centers_y, 'xb')
plt.title('Flower Petal Length against Sepal Length per Species')
plt.ylabel('Petal Length')
plt.xlabel('Sepal Length')
plt.show()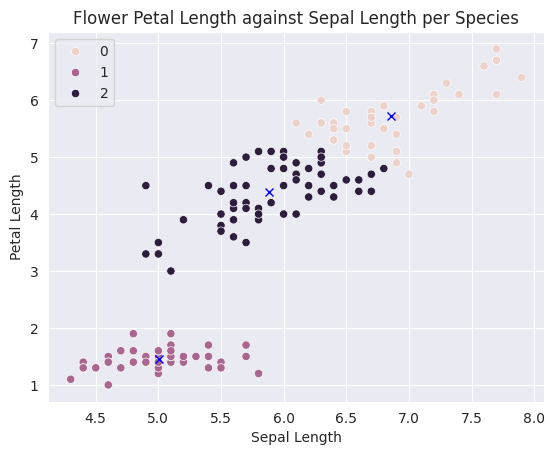

As you can see, K-means algorithm was able to classify (for the most part) different specifies of flowers into separate clusters. Note that we did not provide the “species” column as an input to KMeans.

We can check the “goodness” of the fit by looking at model.inertia_, which contains the sum of squared distances of samples to their closest cluster center. Lower the inertia, better the fit.

model.inertia_

78.8556658259773

Let’s try creating 6 clusters.

model = KMeans(n_clusters=6, random_state=42)
# fitting the model
model.fit(X)
# making predictions on X (clustering)
preds = model.predict(X)
# assign each row to their cluster
X['clusters'] = preds
# looking at some samples
X.sample(n=5)

	sepal_length	sepal_width	petal_length	petal_width	clusters
37	4.9	3.6	1.4	0.1	5
54	6.5	2.8	4.6	1.5	0
2	4.7	3.2	1.3	0.2	1
59	5.2	2.7	3.9	1.4	2
56	6.3	3.3	4.7	1.6	0

Let’s visualize the clusters

sns.scatterplot(data=X, x='sepal_length', y='petal_length', hue=preds)
centers_x, centers_y = model.cluster_centers_[:,0], model.cluster_centers_[:,2]
plt.plot(centers_x, centers_y, 'xb')
plt.title('Flower Petal Length against Sepal Length per Species')
plt.ylabel('Petal Lenght')
plt.xlabel('Sepal Length')
plt.show()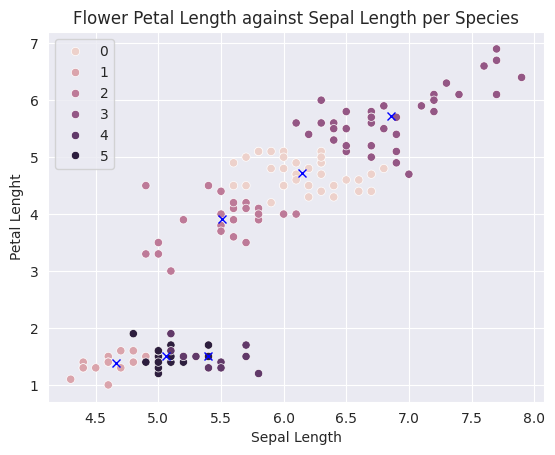

# Let's calculate the new model inertia
model.inertia_

50.560990643274856

So, what number of clusters is good enough?

In most real-world scenarios, there’s no predetermined number of clusters. In such a case, you can create a plot of “No. of clusters” vs “Inertia” to pick the right number of clusters.

options = range(2, 11)
inertias = []

for n_clusters in options:
    model = KMeans(n_clusters, random_state=42).fit(X)
    inertias.append(model.inertia_)
    
plt.plot(options, inertias, linestyle='-', marker='o')
plt.title("No. of clusters vs. Inertia")
plt.xlabel('No. of clusters (K)')
plt.ylabel('Inertia')

Text(0, 0.5, 'Inertia')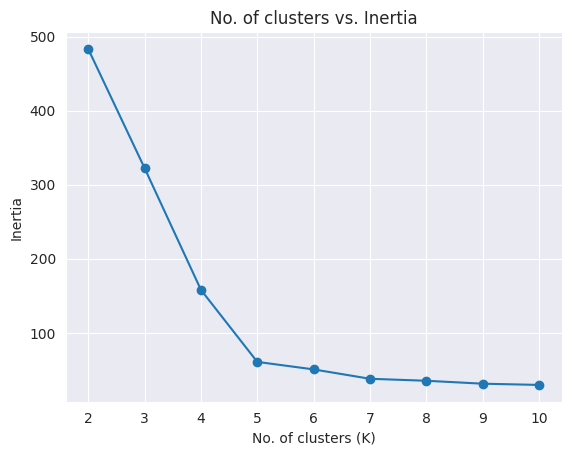

The chart is creates an “elbow” plot, and you can pick the number of clusters beyond which the reduction in inertia decreases sharply.

Mini Batch K Means: The K-means algorithm can be quite slow for really large dataset. Mini-batch K-means is an iterative alternative to K-means that works well for large datasets. Learn more about it here: https://scikit-learn.org/stable/modules/clustering.html#mini-batch-kmeans

EXERCISE: Perform clustering on the Mall customers dataset on Kaggle. Study the segments carefully and report your observations.

Summary and References

Congratulations on finishing this lesson. The following topics were covered in this tutorial:

Overview of unsupervised learning algorithms in Scikit-learn
K Means Clustering

Check out these resources to learn more:

Don’t Miss Any Updates!

Introduction to Unsupervised Learning

Clustering

K Means Clustering

So, what number of clusters is good enough?

Summary and References

What’s on your mind? Put it in the comments!