# These are the libraries we are going to use in the lab.
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits import mplot3d
from dataidea_science.plots import plot_error_surfacesPyTorch build-in functions
Create the Model and Total Loss Function, Train the Model via Batch Gradient Descent

Linear Regression 1D: Training Two Parameter Mini-Batch Gradient Descent
Objective
- How to use PyTorch build-in functions to create a model.
Table of Contents
In this lab, you will create a model the PyTroch way, this will help you as models get more complicated
- Make Some Data
- Create the Model and Cost Function the PyTorch way
- Train the Model: Batch Gradient Descent
Estimated Time Needed: 30 min
Preparation
We’ll need the following libraries:
The class plot_error_surfaces is just to help you visualize the data space and the parameter space during training and has nothing to do with PyTorch.
Make Some Data
Import libraries and set random seed.
# Import libraries and set random seed
import torch
from torch.utils.data import Dataset, DataLoader
torch.manual_seed(1)<torch._C.Generator at 0x7f5c8438a2b0>Generate values from -3 to 3 that create a line with a slope of 1 and a bias of -1. This is the line that you need to estimate. Add some noise to the data:
# Create Data Class
class Data(Dataset):
# Constructor
def __init__(self):
self.x = torch.arange(-3, 3, 0.1).view(-1, 1)
self.f = 1 * self.x - 1
self.y = self.f + 0.1 * torch.randn(self.x.size())
self.len = self.x.shape[0]
# Getter
def __getitem__(self,index):
return self.x[index],self.y[index]
# Get Length
def __len__(self):
return self.lenCreate a dataset object:
# Create dataset object
dataset = Data()Plot out the data and the line.
# Plot the data
plt.plot(dataset.x.numpy(), dataset.y.numpy(), 'rx', label = 'y')
plt.plot(dataset.x.numpy(), dataset.f.numpy(), label = 'f')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()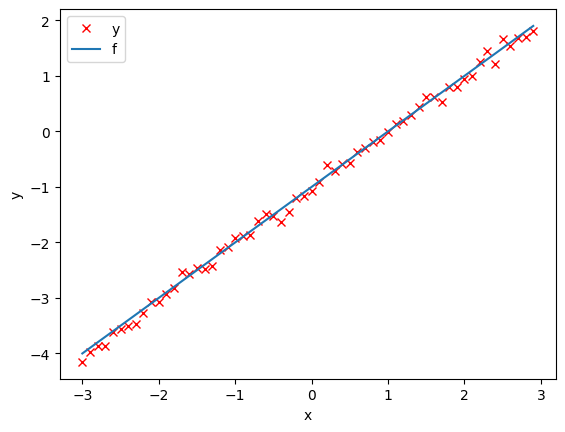
Create the Model and Total Loss Function (Cost)
Create a linear regression class
# Create a linear regression model class
from torch import nn, optim
class linear_regression(nn.Module):
# Constructor
def __init__(self, input_size, output_size):
super(linear_regression, self).__init__()
self.linear = nn.Linear(input_size, output_size)
# Prediction
def forward(self, x):
yhat = self.linear(x)
return yhatNote about the super() method: - When LinearRegression is instantiated, its __init__ method is called. - Inside LinearRegression.__init__, super(LinearRegression, self).__init__() calls the __init__ method of the parent class (nn.Module). - After the parent class is initialized, the rest of the code in the LinearRegression.__init__ method runs too.
This mechanism ensures that the nn.Module class is properly initialized before any additional initialization specific to LinearRegression occurs.
The Loss and Optimizer Functions
We will use PyTorch build-in functions to create a criterion function; this calculates the total loss or cost
# Build in cost function
criterion = nn.MSELoss()Create a linear regression object and optimizer object, the optimizer object will use the linear regression object.
# Create optimizer
model = linear_regression(1,1)
optimizer = optim.SGD(model.parameters(), lr = 0.01)list(model.parameters())[Parameter containing:
tensor([[0.3636]], requires_grad=True),
Parameter containing:
tensor([0.4957], requires_grad=True)]Remember to construct an optimizer you have to give it an iterable containing the parameters i.e. provide model.parameters() as an input to the object constructor
Similar to the model, the optimizer has a state dictionary:
optimizer.state_dict(){'state': {},
'param_groups': [{'lr': 0.01,
'momentum': 0,
'dampening': 0,
'weight_decay': 0,
'nesterov': False,
'maximize': False,
'foreach': None,
'differentiable': False,
'fused': None,
'params': [0, 1]}]}Many of the keys correspond to more advanced optimizers.
Create a Dataloader object:
# Create Dataloader object
trainloader = DataLoader(dataset = dataset, batch_size = 1)PyTorch randomly initialises your model parameters. If we use those parameters, the result will not be very insightful as convergence will be extremely fast. So we will initialise the parameters such that they will take longer to converge, i.e. look cool
# Customize the weight and bias
model.state_dict()['linear.weight'][0] = -15
model.state_dict()['linear.bias'][0] = -10Create a plotting object, not part of PyTroch, just used to help visualize
# Create plot surface object
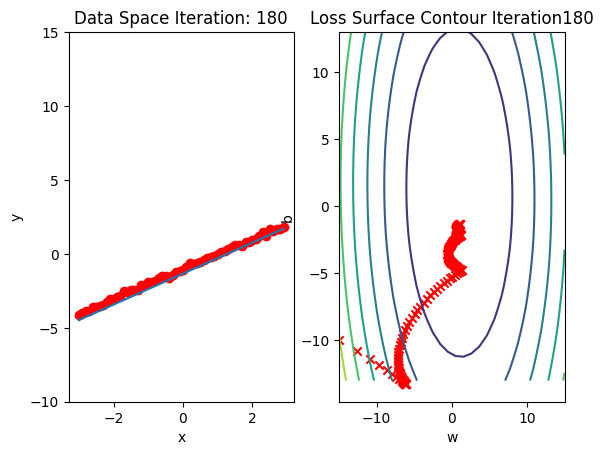
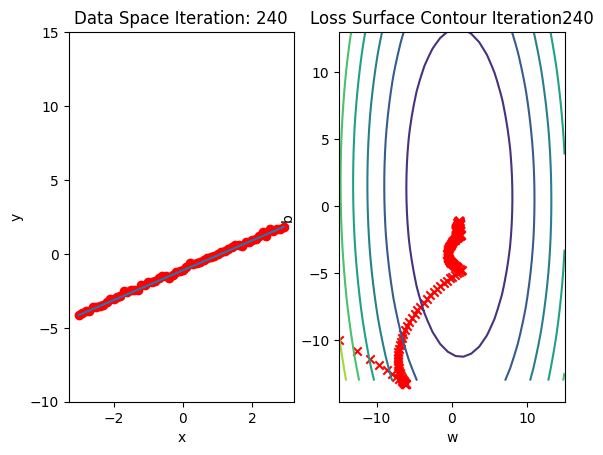
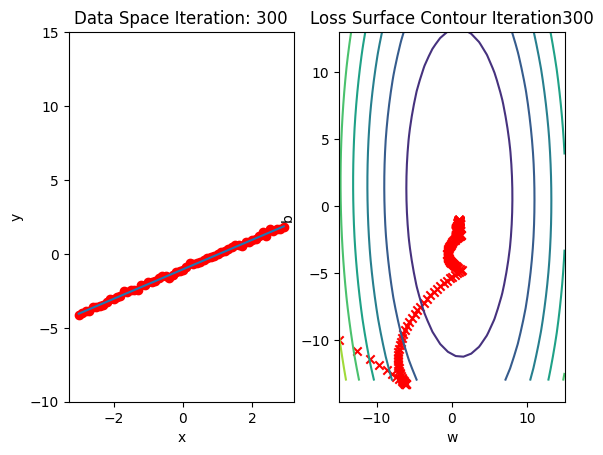
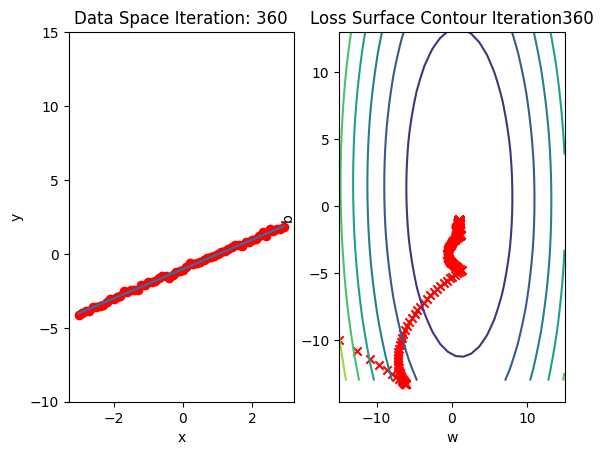
get_surface = plot_error_surfaces(15, 13, dataset.x, dataset.y, 30, go = False)Train the Model via Batch Gradient Descent
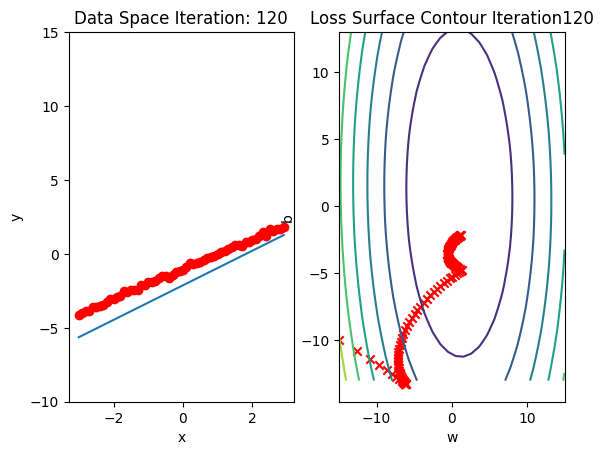
Run 10 epochs of stochastic gradient descent: bug data space is 1 iteration ahead of parameter space.
# Train Model
def train_model_BGD(iter):
for epoch in range(iter):
for x,y in trainloader:
yhat = model(x)
loss = criterion(yhat, y)
get_surface.set_para_loss(model, loss.tolist())
optimizer.zero_grad()
loss.backward()
optimizer.step()
get_surface.plot_ps()
train_model_BGD(10)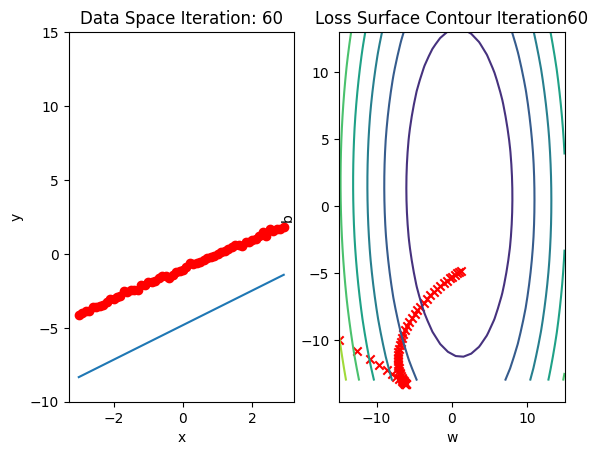
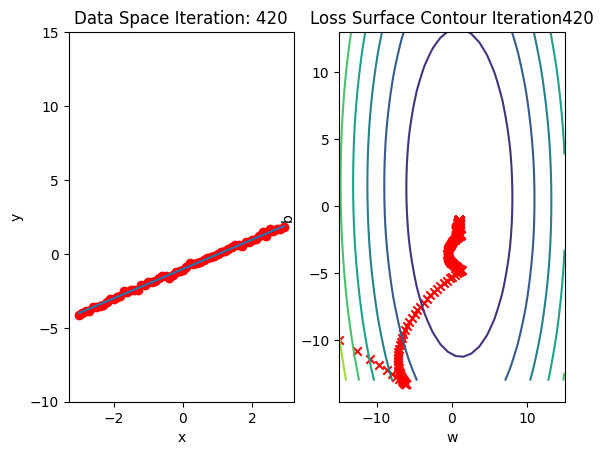
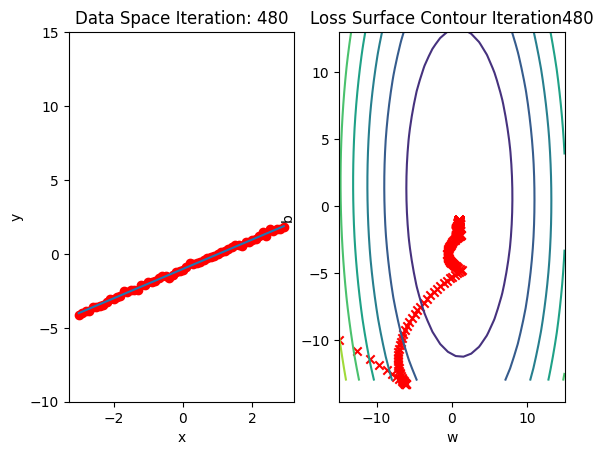
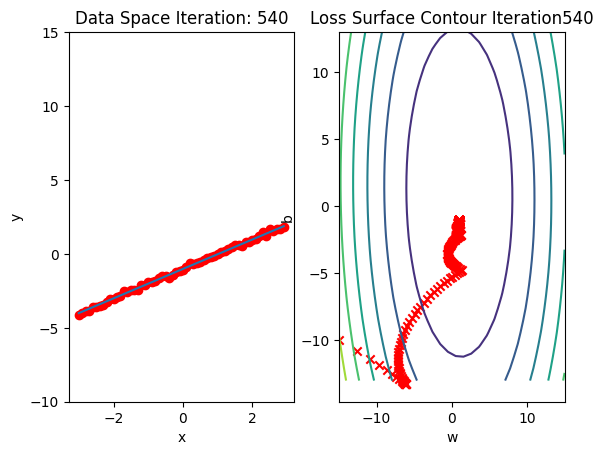
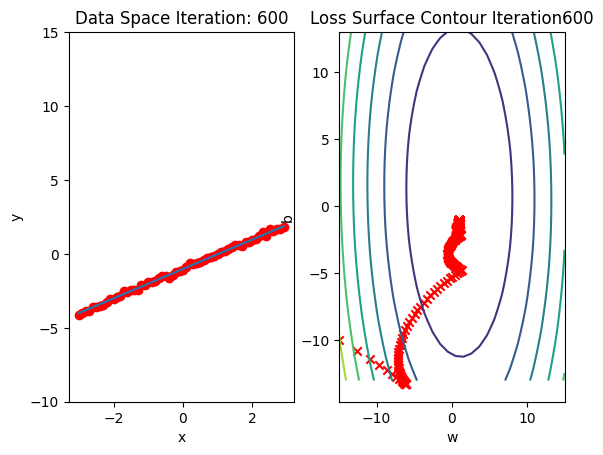
model.state_dict()OrderedDict([('linear.weight', tensor([[0.9932]])),
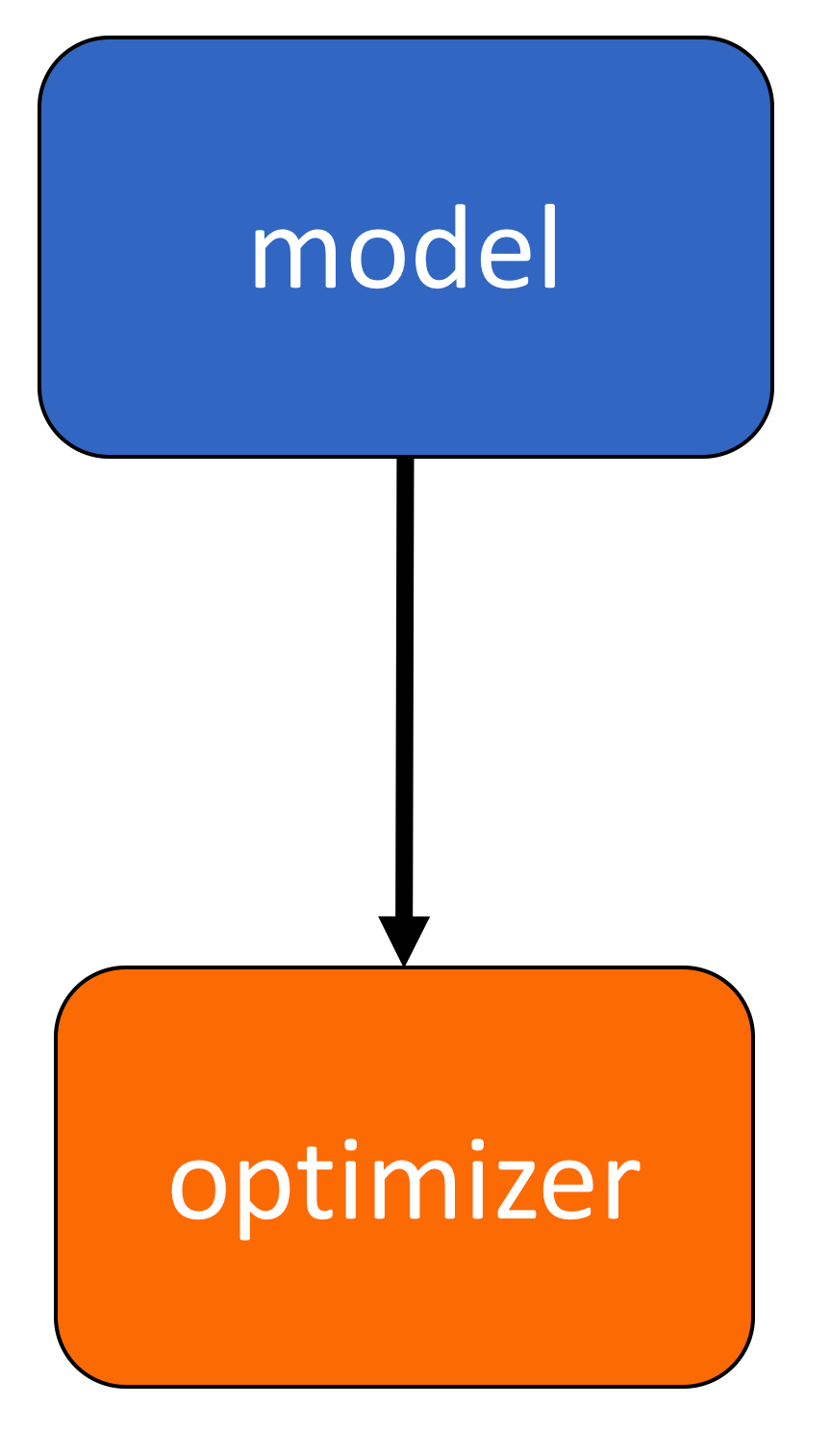
('linear.bias', tensor([-1.0174]))])Let’s use the following diagram to help clarify the process. The model takes x to produce an estimate yhat, it will then be compared to the actual y with the loss function.
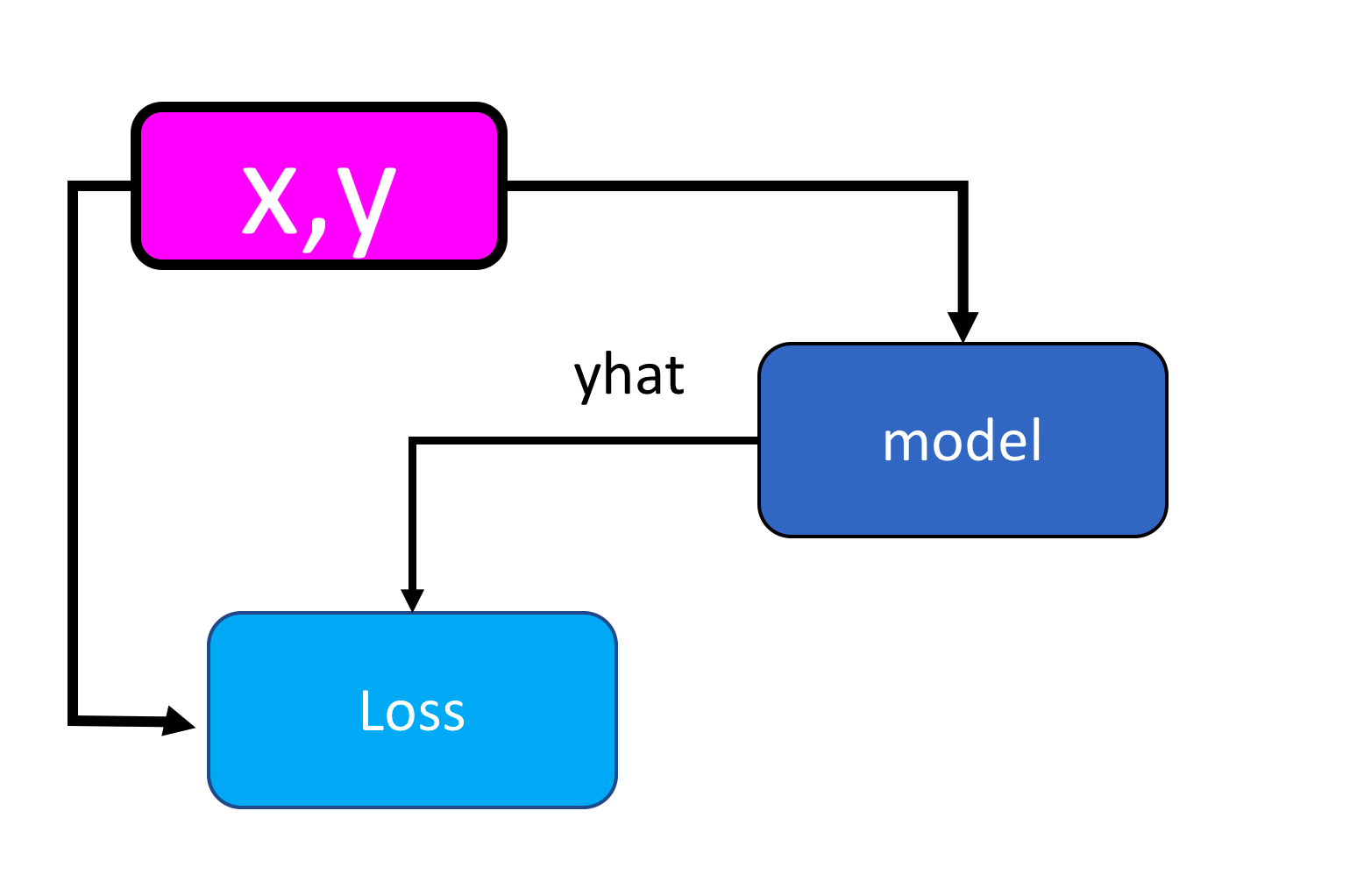
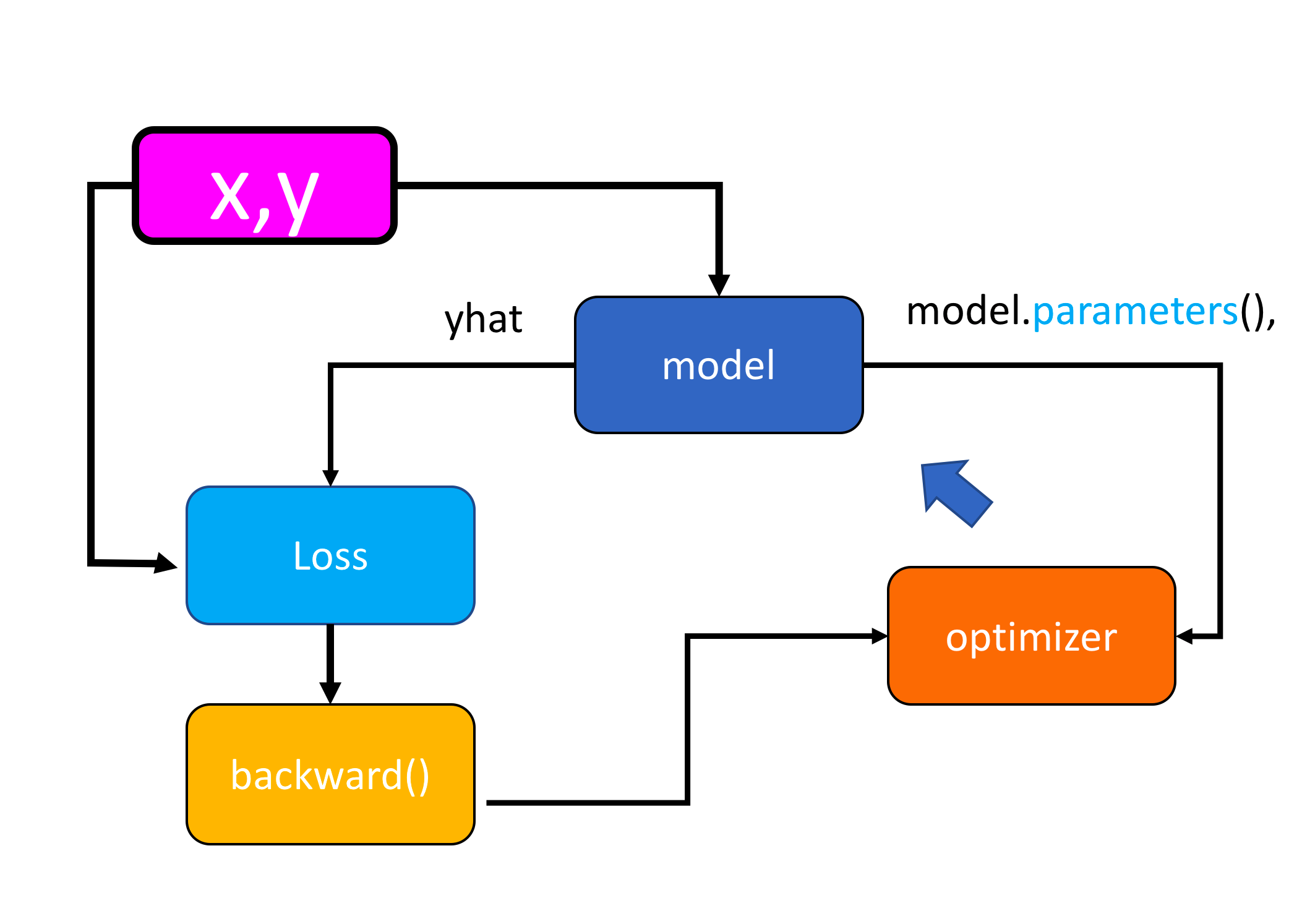
When we call backward() on the loss function, it will handle the differentiation. Calling the method step on the optimizer object it will update the parameters as they were inputs when we constructed the optimizer object. The connection is shown in the following figure :
Practice
Try to train the model via BGD with lr = 0.1. Use optimizer and the following given variables.
# Practice: Train the model via BGD using optimizer
model = linear_regression(1,1)
model.state_dict()['linear.weight'][0] = -15
model.state_dict()['linear.bias'][0] = -10
get_surface = plot_error_surfaces(15, 13, dataset.x, dataset.y, 30, go = False)Double-click here for the solution.