Differentiation in PyTorch

In this lab, you will learn the basics of tensor operations on 2D tensors.

Photo by DATAIDEA

Objective

• How to perform differentiation in pytorch.

Table of Contents

In this lab, you will learn the basics of differentiation.

• Derivatives
• Partial Derivatives

Estimated Time Needed: 25 min

---

Don’t Miss Any Updates!

Before we continue, I have a humble request, to be among the first to hear about future updates of the course materials, simply enter your email below, follow us on (formally Twitter), or subscribe to our YouTube channel.

Preparation

The following are the libraries we are going to use for this lab.

# These are the libraries will be useing for this lab.

import torch 
import matplotlib.pylab as plt

Derivatives

Let us create the tensor x and set the parameter requires_grad to true because you are going to take the derivative of the tensor.

# Create a tensor x

x = torch.tensor(2.0, requires_grad = True)
print("The tensor x: ", x)

The tensor x:  tensor(2., requires_grad=True)

Then let us create a tensor according to the equation \(y=x^2\).

# Create a tensor y according to y = x^2

y = x ** 2
print("The result of y = x^2: ", y)

The result of y = x^2:  tensor(4., grad_fn=<PowBackward0>)

Then let us take the derivative with respect x at x = 2

# Take the derivative. Try to print out the derivative at the value x = 2

y.backward()
print("The dervative at x = 2: ", x.grad)

The dervative at x = 2:  tensor(4.)

The preceding lines perform the following operation:

\(\frac{\mathrm{dy(x)}}{\mathrm{dx}}=2x\)

\(\frac{\mathrm{dy(x=2)}}{\mathrm{dx}}=2(2)=4\)

print('data:',x.data)
print('grad_fn:',x.grad_fn)
print('grad:',x.grad)
print("is_leaf:",x.is_leaf)
print("requires_grad:",x.requires_grad)

data: tensor(2.)
grad_fn: None
grad: tensor(4.)
is_leaf: True
requires_grad: True

print('data:',y.data)
print('grad_fn:',y.grad_fn)
print('grad:',y.grad)
print("is_leaf:",y.is_leaf)
print("requires_grad:",y.requires_grad)

data: tensor(4.)
grad_fn: <PowBackward0 object at 0x7873c29f8070>
grad: None
is_leaf: False
requires_grad: True

/tmp/ipykernel_17856/1355624623.py:3: UserWarning: The .grad attribute of a Tensor that is not a leaf Tensor is being accessed. Its .grad attribute won't be populated during autograd.backward(). If you indeed want the .grad field to be populated for a non-leaf Tensor, use .retain_grad() on the non-leaf Tensor. If you access the non-leaf Tensor by mistake, make sure you access the leaf Tensor instead. See github.com/pytorch/pytorch/pull/30531 for more informations. (Triggered internally at aten/src/ATen/core/TensorBody.h:489.)
  print('grad:',y.grad)

Let us try to calculate the derivative for a more complicated function.

# Calculate the y = x^2 + 2x + 1, then find the derivative 

x = torch.tensor(2.0, requires_grad = True)
y = x ** 2 + 2 * x + 1
print("The result of y = x^2 + 2x + 1: ", y)
y.backward()
print("The dervative at x = 2: ", x.grad)

The result of y = x^2 + 2x + 1:  tensor(9., grad_fn=<AddBackward0>)
The dervative at x = 2:  tensor(6.)

The function is in the following form: \(y=x^{2}+2x+1\)

The derivative is given by:

\(\frac{\mathrm{dy(x)}}{\mathrm{dx}}=2x+2\)

\(\frac{\mathrm{dy(x=2)}}{\mathrm{dx}}=2(2)+2=6\)

Practice

Determine the derivative of \(y = 2x^3+x\) at \(x=1\)

# Practice: Calculate the derivative of y = 2x^3 + x at x = 1

# Type your code here

Double-click here for the solution.

We can implement our own custom autograd Functions by subclassing torch.autograd.Function and implementing the forward and backward passes which operate on Tensors

class SQ(torch.autograd.Function):


    @staticmethod
    def forward(ctx,i):
        """
        In the forward pass we receive a Tensor containing the input and return
        a Tensor containing the output. ctx is a context object that can be used
        to stash information for backward computation. You can cache arbitrary
        objects for use in the backward pass using the ctx.save_for_backward method.
        """
        result=i**2
        ctx.save_for_backward(i)
        return result

    @staticmethod
    def backward(ctx, grad_output):
        """
        In the backward pass we receive a Tensor containing the gradient of the loss
        with respect to the output, and we need to compute the gradient of the loss
        with respect to the input.
        """
        i, = ctx.saved_tensors
        grad_output = 2*i
        return grad_output

We can apply it the function

x=torch.tensor(2.0,requires_grad=True )
sq=SQ.apply

y=sq(x)
y
print(y.grad_fn)
y.backward()
x.grad

<torch.autograd.function.SQBackward object at 0x7873c29c7df0>

tensor(4.)

Partial Derivatives

We can also calculate Partial Derivatives. Consider the function: \(f(u,v)=vu+u^{2}\)

Let us create u tensor, v tensor and f tensor

# Calculate f(u, v) = v * u + u^2 at u = 1, v = 2

u = torch.tensor(1.0,requires_grad=True)
v = torch.tensor(2.0,requires_grad=True)
f = u * v + u ** 2
print("The result of v * u + u^2: ", f)

The result of v * u + u^2:  tensor(3., grad_fn=<AddBackward0>)

This is equivalent to the following:

\(f(u=1,v=2)=(2)(1)+1^{2}=3\)

Now let us take the derivative with respect to u:

# Calculate the derivative with respect to u

f.backward()
print("The partial derivative with respect to u: ", u.grad)

The partial derivative with respect to u:  tensor(4.)

the expression is given by:

\(\frac{\mathrm{\partial f(u,v)}}{\partial {u}}=v+2u\)

\(\frac{\mathrm{\partial f(u=1,v=2)}}{\partial {u}}=2+2(1)=4\)

Now, take the derivative with respect to v:

# Calculate the derivative with respect to v

print("The partial derivative with respect to u: ", v.grad)

The partial derivative with respect to u:  tensor(1.)

The equation is given by:

\(\frac{\mathrm{\partial f(u,v)}}{\partial {v}}=u\)

\(\frac{\mathrm{\partial f(u=1,v=2)}}{\partial {v}}=1\)

Calculate the derivative with respect to a function with multiple values as follows. You use the sum trick to produce a scalar valued function and then take the gradient:

# Calculate the derivative with multiple values

x = torch.linspace(-10, 10, 10, requires_grad = True)
Y = x ** 2
y = torch.sum(x ** 2)

We can plot the function and its derivative

# Take the derivative with respect to multiple value. Plot out the function and its derivative

y.backward()

plt.plot(x.detach().numpy(), Y.detach().numpy(), label = 'function')
plt.plot(x.detach().numpy(), x.grad.detach().numpy(), label = 'derivative')
plt.xlabel('x')
plt.legend()
plt.show()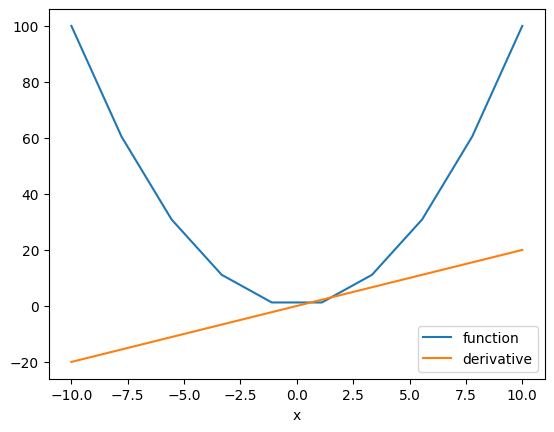

The orange line is the slope of the blue line at the intersection point, which is the derivative of the blue line.

The method detach() excludes further tracking of operations in the graph, and therefore the subgraph will not record operations. This allows us to then convert the tensor to a numpy array. To understand the sum operation Click Here

The relu activation function is an essential function in neural networks. We can take the derivative as follows:

# Take the derivative of Relu with respect to multiple value. Plot out the function and its derivative

x = torch.linspace(-10, 10, 1000, requires_grad = True)
Y = torch.relu(x)
y = Y.sum()
y.backward()
plt.plot(x.detach().numpy(), Y.detach().numpy(), label = 'function')
plt.plot(x.detach().numpy(), x.grad.detach().numpy(), label = 'derivative')
plt.xlabel('x')
plt.legend()
plt.show()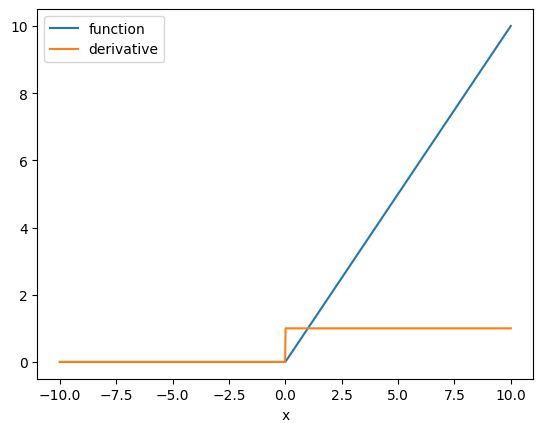

y.grad_fn

<SumBackward0 at 0x7873545dfc40>

Practice

Try to determine partial derivative \(u\) of the following function where \(u=2\) and \(v=1\): $ f=uv+(uv)^2$

# Practice: Calculate the derivative of f = u * v + (u * v) ** 2 at u = 2, v = 1

# Type the code here

What’s on your mind? Put it in the comments!