Linear Regression 1D, Prediction

In this lab, we will review how to make a prediction in several different ways by using PyTorch.

Photo by DATAIDEA

Objective

• How to make the prediction for multiple inputs.
• How to use linear class to build more complex models.
• How to build a custom module.

Table of Contents

In this lab, we will review how to make a prediction in several different ways by using PyTorch.

• Prediction
• Class Linear
• Build Custom Modules

Estimated Time Needed: 15 min

---

Don’t Miss Any Updates!

Before we continue, I have a humble request, to be among the first to hear about future updates of the course materials, simply enter your email below, follow us on (formally Twitter), or subscribe to our YouTube channel.

Preparation

The following are the libraries we are going to use for this lab.

# These are the libraries will be used for this lab.

import torch

Prediction

Let us create the following expressions:

\(b=-1,w=2\)

\(\hat{y}=-1+2x\)

First, define the parameters:

# Define w = 2 and b = -1 for y = wx + b

w = torch.tensor(2.0, requires_grad = True)
b = torch.tensor(-1.0, requires_grad = True)

Then, define the function forward(x, w, b) makes the prediction:

# Function forward(x) for prediction

def forward(x):
    yhat = w * x + b
    return yhat

Let’s make the following prediction at x = 1

\(\hat{y}=-1+2x\)

\(\hat{y}=-1+2(1)\)

m = torch.tensor([2])
print(m)

forward(m)

tensor([2])

tensor([3.], grad_fn=<AddBackward0>)

# Predict y = 2x - 1 at x = 1

x = torch.tensor([[1.0]])
yhat = forward(x)
print("The prediction: ", yhat)

The prediction:  tensor([[1.]], grad_fn=<AddBackward0>)

Now, let us try to make the prediction for multiple inputs:

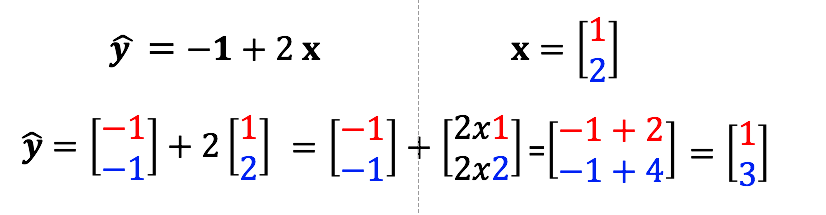
Let us construct the x tensor first. Check the shape of x.

# Create x Tensor and check the shape of x tensor

x = torch.tensor([[1.0], [2.0]])
print("The shape of x: ", x.shape)

The shape of x:  torch.Size([2, 1])

Now make the prediction:

# Make the prediction of y = 2x - 1 at x = [1, 2]

yhat = forward(x)
print("The prediction: ", yhat)

The prediction:  tensor([[1.],
        [3.]], grad_fn=<AddBackward0>)

The result is the same as what it is in the image above.

Practice

Make a prediction of the following x tensor using the w and b from above.

# Practice: Make a prediction of y = 2x - 1 at x = [[1.0], [2.0], [3.0]]

x = torch.tensor([[1.0], [2.0], [3.0]])
yhat = forward(x)
print("The prediction: ", yhat)

The prediction:  tensor([[1.],
        [3.],
        [5.]], grad_fn=<AddBackward0>)

Double-click here for the solution.

Class Linear

The linear class can be used to make a prediction. We can also use the linear class to build more complex models. Let’s import the module:

# Import Class Linear

from torch.nn import Linear

Set the random seed because the parameters are randomly initialized:

# Set random seed

torch.manual_seed(1)

<torch._C.Generator at 0x7c780c384eb0>

Let us create the linear object by using the constructor. The parameters are randomly created. Let us print out to see what w and b. The parameters of an torch.nn.Module model are contained in the model’s parameters accessed with lr.parameters():

# Create Linear Regression Model, and print out the parameters

lr = Linear(in_features=1, out_features=1, bias=True)
print("Parameters w and b: ", list(lr.parameters()))

Parameters w and b:  [Parameter containing:
tensor([[0.2772]], requires_grad=True), Parameter containing:
tensor([-0.3058], requires_grad=True)]

This is equivalent to the following expression:

\(b=-0.44, w=0.5153\)

\(\hat{y}=-0.44+0.5153x\)

A method state_dict() Returns a Python dictionary object corresponding to the layers of each parameter tensor.

print("Python dictionary: ",lr.state_dict())
print("keys: ",lr.state_dict().keys())
print("values: ",lr.state_dict().values())

Python dictionary:  OrderedDict({'weight': tensor([[0.3652]]), 'bias': tensor([-0.3897])})
keys:  odict_keys(['weight', 'bias'])
values:  odict_values([tensor([[0.3652]]), tensor([-0.3897])])

The keys correspond to the name of the attributes and the values correspond to the parameter value.

print("weight:",lr.weight)
print("bias:",lr.bias)

weight: Parameter containing:
tensor([[0.3652]], requires_grad=True)
bias: Parameter containing:
tensor([-0.3897], requires_grad=True)

Now let us make a single prediction at x = [[1.0]].

# Make the prediction at x = [[1.0]]

x = torch.tensor([[1.0]])
yhat = lr(x)
print("The prediction: ", yhat)

The prediction:  tensor([[-0.0245]], grad_fn=<AddmmBackward0>)

Similarly, you can make multiple predictions:

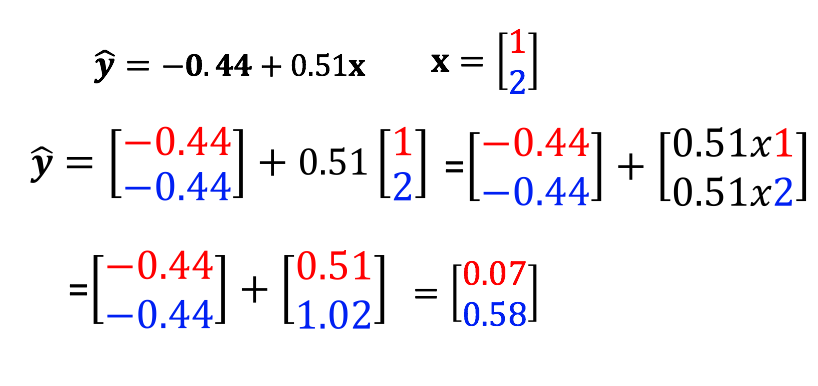
Use model lr(x) to predict the result.

# Create the prediction using linear model

x = torch.tensor([[1.0], [2.0]])
yhat = lr(x)
print("The prediction: ", yhat)

The prediction:  tensor([[-0.0286],
        [ 0.2487]], grad_fn=<AddmmBackward0>)

Practice

Make a prediction of the following x tensor using the linear regression model lr.

# Practice: Use the linear regression model object lr to make the prediction.

x = torch.tensor([[1.0],[2.0],[3.0]])
yhat = lr(x)

print("The prediction: ", yhat)

The prediction:  tensor([[-0.0286],
        [ 0.2487],
        [ 0.5259]], grad_fn=<AddmmBackward0>)

Double-click here for the solution.

Build Custom Modules

Now, let’s build a custom module. We can make more complex models by using this method later on.

First, import the following library.

# Library for this section

from torch import nn

Now, let us define the class:

# Customize Linear Regression Class

class LR(nn.Module):
    
    # Constructor
    def __init__(self, input_size, output_size):
        
        # Inherit from parent
        super(LR, self).__init__()
        self.linear = nn.Linear(input_size, output_size)
    
    # Prediction function
    def forward(self, x):
        out = self.linear(x)
        return out

Create an object by using the constructor. Print out the parameters we get and the model.

# Create the linear regression model. Print out the parameters.

lr = LR(1, 1)
print("The parameters: ", list(lr.parameters()))
print("Linear model: ", lr.linear)

The parameters:  [Parameter containing:
tensor([[-0.0729]], requires_grad=True), Parameter containing:
tensor([-0.0900], requires_grad=True)]
Linear model:  Linear(in_features=1, out_features=1, bias=True)

Let us try to make a prediction of a single input sample.

# Try our customize linear regression model with single input

x = torch.tensor([[1.0]])
yhat = lr(x)
print("The prediction: ", yhat)

The prediction:  tensor([[-0.1629]], grad_fn=<AddmmBackward0>)

Now, let us try another example with multiple samples.

# Try our customize linear regression model with multiple input

x = torch.tensor([[1.0], [2.0]])
yhat = lr(x)
print("The prediction: ", yhat)

The prediction:  tensor([[-0.1629],
        [-0.2358]], grad_fn=<AddmmBackward0>)

the parameters are also stored in an ordered dictionary :

print("Python dictionary: ", lr.state_dict())
print("keys: ",lr.state_dict().keys())
print("values: ",lr.state_dict().values())

Python dictionary:  OrderedDict([('weight', tensor([[0.5153]])), ('bias', tensor([-0.4414]))])
keys:  odict_keys(['weight', 'bias'])
values:  odict_values([tensor([[0.5153]]), tensor([-0.4414])])

Practice

Create an object lr1 from the class we created before and make a prediction by using the following tensor:

# Practice: Use the LR class to create a model and make a prediction of the following tensor.

x = torch.tensor([[1.0], [2.0], [3.0]])
lr1 = LR(1, 1)
yhat = lr(x)
yhat
# print("The prediction: ", yhat)

tensor([[-0.1629],
        [-0.2358],
        [-0.3088]], grad_fn=<AddmmBackward0>)

What’s on your mind? Put it in the comments!